Introduction to Statistics – Correlation

Video transcript

1. Start of transcript. Skip to the end.
2. Let’s talk about covariance and correlation.
3. There’s a company that rents bikes and scooters to commuters.
4. And people get to choose either a bike or a scooter,
5. whichever they want.
6. And as it turns out, there’s a negative correlation between
7. the number of bike customers and the number of scooter customers.
8. So what does that actually mean?
9. So you can see a negative correlation in the scatter plot
10. clearly, but
11. what is the technical definition of correlation?
12. Well, let’s think about it this way.
13. So this is the average number of scoot customers per day here,
14. and here’s the average number of bike customers.
15. So what it says is that if there are more than average scoot
16. customers on a particular day, there are probably fewer
17. than average bike customers and vice versa.
18. Okay, so there that is.
19. Higher than average scoot corresponds to lower than
20. average bike, right, higher than average scoot and
21. lower than average bike.
22. Okay, so, vice versa, if Monster Scoot has fewer customers than
23. their usual average, it probably means Monster Bike has higher
24. than average number of customers that day.
25. And so that brings me to a formal definition of
26. covariance and correlation.
27. Let’s start with covariance.
28. Okay, so let’s say whether X is above or below its mean.
29. And I’m writing the mean here, the mean of X,
30. as the expectation of X.
31. And I used the notation mu before, but
32. this means the same thing.
33. And this notation is just as common as the mu notation.
34. So we’re looking at whether X is above or below its mean.
35. And now let’s see if Y is above or below its mean.
36. So two random variables, X and Y,
37. if X is higher than its mean when Y is lower than its mean,
38. then this thing is gonna be negative.
39. Actually let’s just go through all the combinations.
40. So if X is higher than its mean and
41. Y is higher than its mean, then this is positive.
42. Now, if X is above its mean, and Y is below its mean, when you
43. multiply them together, you get something that’s negative.
44. And I filled in the rest.
45. Now if X is below its mean when Y is below its mean,
46. we’re gonna be multiplying two negative numbers together, and
47. then we’ll get a positive one.
48. Okay, so this is the definition of the covariance.
49. It’s just the expectation of this quantity in here.
50. So, now it’s all about how often things happen.
51. If we’re often in a situation where X and Y vary together,
52. then the product in here will often be positive,
53. and then the expectation will be positive.
54. Okay, so that’s for the population.
55. What if you only have data?
56. Then you need to compute the sample covariance which is
57. this thing down here.
58. It’s exactly the same thing as the covariance.
59. The only difference is that you can compute it from your data
60. which is 1 to n.
61. And then again there’s this mysterious n-1 over there that
62. you really should not pay attention to cuz it’s just
63. an issue of bias.
64. Like I said, it’s already in the software to compute that for
65. you so you shouldn’t pay attention to it.
66. Then what happens if you take the covariance of X with itself?
67. So X, the Y is also equal to X.
68. Look at this, does that look familiar?
69. It should, because it is exactly the variance, and
70. this is the same definition we had earlier.
71. Take the distance of X from its mean,
72. square it to get the squared distance from the mean, and
73. take the expectation, and that’s the variance.
74. And then this one here is the sample variance, again,
75. with that silly n-1 over there.
76. And the sample variance has a particular notation, and
77. it is called s squared.
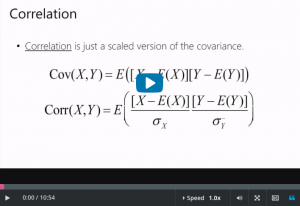
78. Now the issue with covariance is that it’s not in units that make
79. any sense.
80. So correlation is a version of covariance, but where we scaled
81. its value so that the largest possible correlation is one,
82. and the smallest possible value is minus one.
83. And so that’s what these terms are here.
84. So this is the standard deviation of X, and
85. this is the standard deviation of Y.
86. And when you scale this quantity by these two terms, then
87. the largest value is one and the smallest value is minus one.
88. Okay, and here is the sample correlation.
89. And again, you get that silly n-1 term.
90. And then these become quantities that you can compute from your
91. data, namely the sample standard deviations of X and of Y.
92. Now since correlations are always between +1 and
93. -1, a correlation of 0.7 say, that’s actually meaningful.
94. I can really understand it on this scale between 1 and -1.
95. Here’s a nice plot showing some of the data from the automobile
96. pricing data set.
97. Now each car in this data set gets a dot which represents its
98. price, and then the size of the engine of the car.
99. And you can definitely see that there’s
100. a clear positive correlation there.
101. As price goes up,
102. you would definitely expect the engine size of a car to go up.
103. If you paid more for the car, you’re paying for
104. a bigger engine.
105. And the increase pretty much follows a straight line here.
106. And it follows the straight line well enough
107. that the correlation is actually 0.89.
108. See the covariance here, that’s in weird units, so it’s really
109. hard to figure out what that number means intuitively.
110. But the correlation,
111. that’s actually much easier to deal with.
112. And then here’s more of that same data set, so this is bore
113. diameter which is the size of a part of the engine, and price.
114. This bore diameter, it does correlate with price, but
115. it’s not as closely correlated as the engine size.
116. So here the correlation is 0.55, and again I have this mysterious
117. covariance value that I don’t know exactly what to do with.
118. Now this is city miles per gallon versus price,
119. and here you can see a negative correlation.
120. I guess that as price goes up the cars must not be as
121. efficient, probably because they have bigger engines or
122. something, I don’t know.
123. Anyway, so the correlation is -0.7.
124. And that again that’s meaningful because the lowest it can be is
125. a -1.
126. Now be careful because people widely confuse
127. correlation with causation.
128. Correlation is really, really not causation.
129. And here is the quintessential example of why that’s not true.
130. It turns out that health, human health,
131. has a negative correlation with how wealthy you are.
132. So you see points like this.
133. If you plot sort of the individuals around the world,
134. you’ll notice that the healthier they are, the less wealthy they
135. are, and the more wealthy they are, the less healthy they are.
136. So why in the world is that?
137. And if you think for a minute, you’ll figure it out.
138. And you’ll figure out that there is some piece of information I
139. didn’t tell you, which is the age of these individuals.
140. Because older people tend to be wealthier but less healthy, and
141. younger people tend to be not as wealthy, but
142. definitely more healthy.
143. So what does that mean?
144. This is not causal.
145. It doesn’t mean that poor health causes you to be rich.
146. And it also doesn’t mean that being rich causes you to be
147. unhealthy.
148. There’s nothing causal here.
149. But there’s a correlation.
150. I can predict health from wealth.
151. I can predict wealth from health without anything causal in there
152. at all.
153. Now in machine learning, which we’ll get to,
154. prediction is the name of the game.
155. It’s not causality necessarily.
156. There are some special branches of machine learning that
157. are sort of concerned with causality.
158. But for the most part,
159. machine learning is just about predicting the future from data,
160. not necessarily understanding the causal mechanisms.
161. And so that’s a longer discussion that
162. I really don’t wanna get into too much here.
163. It’s just nice,
164. though, that you don’t have to worry about causality because
165. not having to worry about that makes things much
166. easier from a practical perspective.
167. You can just predict without worrying about the causes.
168. So let’s say that you’re trying to predict whether someone will
169. want a coupon for your store.
170. But you don’t have to worry about why they will take that
171. coupon or why they might want the product.
172. All you have to do is use correlations to guess whether
173. she might want the coupon.
174. So for instance you could say, it’s Tuesday, and
175. she often takes coupons on Tuesdays.
176. So let’s enter a coupon.
177. Who cares why she likes coupons on Tuesdays,
178. we just know she does.
179. Or we could say, people like her want this coupon,
180. so let’s send it to her.
181. Now machine learning is all about combining the right
182. correlations to be able to predict accurately.
183. But you can’t make conclusion about causality unless you learn
184. more about causal inference techniques, which is really for
185. another day.
186. End of transcript. Skip to the start.